투수가 홈런 캐치를 할 수 있을까?

글에 들어가기에 앞서, 제목이 뜻하는 바가 명확히 전달되지 않을지도 모르겠다. 필자의 의문은 ‘건드리지 않았다면 라인드라이브로 날아가 중앙 펜스를 넘겼을 타구를, 투수가 팔을 뻗어 잡을 수 있는가’ 하는 것이다. 물론 외야수가 아닌 다른 선수가 홈런을 잡는다는 것은 다소 황당하게 들린다. 특히 투수는 총알같이 빠른 공을 던지는 데만 익숙하지, 총알같이 빠른 타구를 잡는 데 익숙한 사람들이 아니다.

하지만 투수가 홈런 캐치를 하기에 최적화된 조건을 가정한다면 어떨까? 혹시 투구 직후에 글러브를 뻗어 슈퍼맨 캐치를 하는 일이 가능하지 않을까? 이 글에서는 a. 투수가 잡을 수 있는 타구 중 최고 속도와 최대 발사 각도를 결정 b. 이 타구가 담장을 넘기기 위한 외부 조건(구장, 날씨) 및 기타 요소(타구 회전량)를 가정하는 순서로 사고 실험을 진행해 보고자 한다.

1. 타구 속도

라인드라이브 타구가 담장을 넘어가기 위해서는 우선 속도가 엄청나게 빨라야 할 것이다. 스탯캐스트 시대(2015년 이후)의 가장 빠른 타구 속도 기록은 지안카를로 스탠튼이 가지고 있는데, 마이애미 소속이었던 2017년에 시속 122.2마일, 즉 196.7km/h의 타구를 쳐낸 적이 있다. 따라서 실험 속 타구의 속도를 196.7km/h라 가정하자.

2. 발사 각도​​

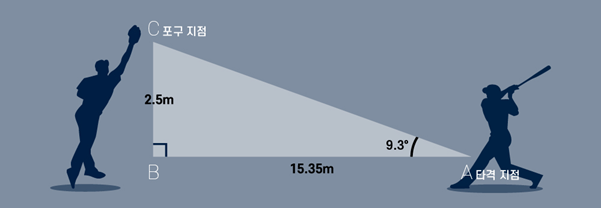
땅볼/라인드라이브 타구(발사 각도 25도 미만 타구)의 속도가 일정할 때, 일반적으로 발사 각도가 클수록 비거리 역시 증가한다. 공과 배트가 만나는 지점(A), 투수의 몸에서 A와 높이가 같은 지점(B), 투수가 공을 잡는 지점(C)을 꼭짓점으로 하는 직각삼각형을 그린다. 선분 AB의 길이와 선분 BC의 길이를 알면 발사 각도인 ∠ BAC의 크기를 구할 수 있다. 선분 AB는 짧을수록, 선분 BC는 길수록 발사 각도가 커진다.

선분 AB의 길이를 구하기 위해서 먼저 실험의 대상이 돼 줄 투수를 선정해야 한다. 장신의 투수가 단신의 투수보다 홈런 캐치를 할 가능성이 더 높은 것은 당연하다. 2019년 기준 메이저리그에서 가장 키가 큰 투수는 타일러 글래스노우로, 프로필 상의 신장이 2.03m다. 따라서 이 글에서는 타일러 글래스노우를 실험체로 삼기로 한다.

홈플레이트 기준점(뒤쪽 끝)에서 투구판까지의 거리는 18.44m(6.6피트)다. 하지만 투수는 제자리에 서서 공을 던지는 게 아니라, 자유발을 앞으로 내딛으며 투구한다. 투구판에서 릴리스포인트까지의 거리(지면 기준)를 익스텐션이라고 하는데, 글래스노우는 2019년 9월 27일 로저스 센터에서 무려 2.56m의 익스텐션을 기록한 적이 있다.

우리가 구하고자 하는 값은 투구판에서 디딤발까지의 거리(스트라이드)인데, 이 값은 익스텐션보다는 조금 짧다. 글래스노우가 공을 릴리스하는 순간을 찍은 위의 사진을 보면 오른손 끝과 왼발 끝의 지면 상 위치에 5cm 가량 차이가 있다. 따라서 글래스노우의 스트라이드를 2.56-0.05=2.51(m)이라 하자.

그리고 타자 역시 반드시 홈플레이트 기준점에서 공을 때리는 것은 아니다. 배터 박스 앞쪽에 자리를 잡고 타격을 하는 타자들은 기준점으로부터 약 58cm, 즉 홈플레이트 앞쪽 끝변으로부터 약 6cm 떨어진 위치에서 공을 때리기도 한다. 그러므로 선분 AB의 길이를 18.44-2.51-0.58=15.35(m)로 잡는다.

이제 선분 BC의 길이를 계산해 보자. 그러기 위해서는 꼭짓점 A(타격 지점)와 꼭짓점 C(포구 지점)의 높이를 알아야 한다(꼭짓점 A와 B의 높이는 같다).

우리의 목표는 선분 BC를 최대한 늘이는 것이므로 타격 지점의 높이가 낮을수록 유리하다. 스탯캐스트 시대에 가장 낮은 공을 쳐서 홈런으로 만든 타자는 오두벨 에레라였는데, 그는 2017년 애틀랜타의 선트러스트 파크에서 22cm 높이의 공을 퍼올려 우측 담장을 넘기는 홈런을 만들어냈다. 하지만 에레라의 홈런은 타구 속도가 162.2km/h밖에 되지 않았다. 이 글에서 글래스노우가 잡아야 할 타구의 속도는 196.7km/h인데, 트래킹 데이터를 분석해 본 결과 이렇게 빠른 타구를 만들어 내기 위해서는 최소 30cm(1피트)의 높이에서 타격이 이루어져야 한다. 그러므로 꼭짓점 A의 높이를 30cm라 가정하자.

그렇다면 투수가 공을 잡는 지점(꼭짓점 C)의 최대 높이는 몇cm일까? 투구판에서 2.51m 떨어진 지점(글래스노우의 디딤발 위치)의 마운드 높이는 약 6cm다. 따라서 글래스노우가 투구 직후에 팔을 뻗어 닿을 수 있는 최대 높이는 203+6+α(cm)다. α를 구하기 위해 키가 174cm인 필자가 글러브를 끼고 직접 실험을 해 보았는데, 머리 위로 팔을 뻗었을 때 최대 225cm 지점까지 닿았다(α=225-174=51). 글래스노우는 필자보다 팔이 훨씬 길고(글래스노우의 전 소속팀 피츠버그의 투수코치였던 레이 시라지는 그의 윙스팬이 2.4m에 달한다고 말한 바 있다), 글러브 사이즈도 클 것이 확실하므로 α를 71로 잡는다. 그러므로 투구 직후 글래스노우의 왼팔이 닿을 수 있는 최대 높이는 203+6+71=280cm다. 위로부터 선분 BC의 길이는 2.8-0.3=2.5(m)라는 결론이다.

선분 AB와 선분 BC의 길이로부터 ∠ BAC(발사 각도)를 계산하면 약 9.3도가 나온다.

9.3도의 발사 각도로 쏘아 올린 196.7km/h의 타구는 얼마나 멀리 날아갈까? 정확한 답은 아직 알 수 없지만, 과거의 비슷한 타구를 찾으면 힌트를 얻을 수 있다. 스탯캐스트 시대에 9.3도의 발사 각도로 196.7km/h에 가장 근접한 타구 속도를 기록한 건 스탠튼이다. 그는 2015년 마이애미의 말린스 파크에서 186.7km/h 속도의 라인드라이브 안타를 쳐냈다. 이 타구는 좌측 파울라인을 타고 약 73.5m(241피트)를 날아간 뒤 지면에 떨어졌다. 우리의 타구가 스탠튼의 2015년 타구보다 정확히 10km/h 더 빠르다는 것을 감안해도, 홈런이 되기에는 비거리가 턱없이 부족하다.

3. 구장

투수가 잡을 수 있는 라인드라이브 타구는 거의 100% 필드 중앙으로 향하는 타구다. 이것은 홈런 캐치를 하려는 글래스노우에게 좋지 않은 소식인데, 대부분의 야구장은 중앙 펜스가 좌우 펜스보다 훨씬 멀기 때문이다.

메이저리그에서 중월 홈런을 치기 가장 쉬운 구장 중 하나는 로스앤젤레스에 위치한 다저 스타디움으로, 중앙 펜스 ↔ 홈의 거리가 약 120.4m(395피트)다. 펜스 높이(2.4m)까지 고려해야 하기 때문에 홈런이 되기 위한 타구 비거리(타구가 구장 구조물에 방해받지 않는다고 가정할 때 낙구 지점으로부터 홈플레이트까지의 거리)는 120.4m보다 더 길어야 한다. 우리의 타구는 추정 비거리가 73.5m 안팎이므로, 중견수가 호세 칸세코가 아닌 이상 절대 중앙 펜스를 넘어갈 수 없을 것으로 보인다. 하지만 아직 고려하지 않은 변수들이 있다.

4. 역회전과 기상 조건

타구의 비거리에 영향을 미치는 요소는 여러 가지가 있다. 발사 각도와 타구 속도가 가장 중요하지만, 고도·바람·기온·습도 등의 외부 요인에 의해서도 비거리는 꽤나 달라질 수 있다. 이에 더해 타구에 회전이 어느 방향으로, 얼마나 많이 걸려 있는지도 따져봐야 한다.

일리노이 대학의 앨런 네이선 박사가 운영하는 The Physics of Baseball 웹사이트에서는 타구 궤적 계산기(Trajectory Calculator)를 제공한다. 이 계산기에 타구의 속도 및 발사 각도, 회전방향 및 회전량, 풍향 및 풍속, 고도, 기온, 습도 등을 넣으면 타구의 궤적과 비거리가 나온다.

먼저 타구 자체의 물리적인 특성부터 확정해 보자. 타구 속도와 발사 각도는 앞에서 이미 결정되었지만 회전량이 아직 미지수로 남아 있다. 적당한 수준의 역회전은 중력과 반대 방향의 마그누스 힘을 발생시켜 야구공의 비행을 도와준다. 애리조나 대학의 A. 테리 베이힐 박사는 자신의 저서 The Science of Baseball: Modeling Bat-Ball Collisions and the Flight of the Ball에서 표준적인 MLB 라인드라이브 타구의 역회전량이 1800~2500rpm이라고 언급했다. 이를 참고하여 글래스노우가 잡아야 할 타구의 역회전량을 1800과 2500의 평균값인 2150rpm이라 가정하자(역회전이 아닌 다른 종류의 회전은 걸려 있지 않다).

다음은 환경과 기상 조건을 설정할 차례다. 다저 스타디움의 해발 고도는 159m(522피트)고, 그에 따른 대기압은 약 30inHg이다. 또한 바람은 플라이볼의 비거리를 상당히 늘려줄 수 있는데, 마음 같아선 로스앤젤레스에 허리케인이 상륙했다고 하고 싶지만 그렇게 강한 바람이 부는 날에는 야구 경기가 진행되기 힘들 것이다. 따라서 가벼운 산들바람 정도인 16.1km/h(시속 10마일)의 바람이 홈에서 외야 중앙 쪽으로 불고 있다고 가정하자(참고로 스탠튼이 73.5m짜리 타구를 친 경기는 지붕을 닫은 돔구장에서 진행되었으므로 바람이 없었다). 마지막으로 최적의 기온과 습도를 찾기 위해 여러 값들을 넣어 본 결과, 기온은 약 섭씨 13도, 습도는 약 30퍼센트일 때 비거리가 가장 큰 것으로 나왔다.

위의 값들을 타구 궤적 계산기에 넣으면, 비거리가 약 128.4m인 것으로 나온다. 또한 펜스가 있는 120.4m 지점에서의 타구 높이는 펜스 높이와 같은 2.4m다. 이로써 글래스노우가 잡을 수 있는 홈런 타구가 완성되었다.

결론

실제 야구 경기에서 투수가 홈런 캐치를 하는 장면을 볼 수 있을까? 몇 백 년 후, 유전 과학의 발달로 배트를 젓가락처럼 휘두르는 타자와 키 3m짜리 투수가 등장하지 않는 이상 불가능에 가까운 일일 것이다. 이 글에서 한 가정들만 보더라도 ’30cm 높이에서 때린 196.7km/h의 타구’가 필요한 데다가, 글래스노우에게 초인적인 반사신경을 요구하고 있다. 여기에 스탠튼이 양키스에서 먹튀짓을 하다가 다저스로 트레이드돼야 한다는 전제 조건까지 붙어 있다(다저스에게 스탠튼의 엄청난 연봉을 감당할 능력이 있다면 말이다). 그리고 글래스노우가 역사상 가장 위대한 캐치를 해낸다고 해도, 타구는 어차피 탬파베이의 중견수 케빈 키어마이어에게 잡힐 운명이었는지도 모른다. 키어마이어는 다저 스타디움보다 펜스가 더 높은 구장에서도 여러 차례 홈런을 훔쳐낸 바 있다.

하지만 사고 실험 속에서만이라도 투수가 홈런 캐치를 할 수 있음을 아는 것은 즐겁다. 어릴 적 동네 야구에서 투수를 해 본 사람이라면, 외야수가 없어서 평범한 플라이볼이 장타가 돼 야속해 했던 경험이 있을 것이다. 그러나 외야수가 왜 필요한가? 투수 본인이 홈런까지 잡아버릴 수 있는 것을.

(이 글은 야구공작소에 계신 많은 분들의 도움을 받아 탄생할 수 있었다. 글의 내용과 관련해 여러 가지 조언을 해 주신 홍기훈, 도상현 님께 특별히 감사의 말씀을 전한다.)

야구공작소 나상인 칼럼니스트

에디터=야구공작소 도상현

도움=야구공작소 홍기훈, 오연우

일러스트=야구공작소 이찬희

​GIF 출처=엠비씨스포츠플러스, mlb.com

사진 출처=tampabay.com/sports/rays/, blog.naver.com/bestbox, chicagomag.com/city-life/

참조=mlb.com, baseballsavant.com, baseballreference.com

© 야구공작소. 출처 표기 없는 무단 전재 및 재배포를 금합니다. 상업적 사용은 별도 문의 바랍니다.

​