오타니 vs 오타니

2021시즌 메이저리그 아메리칸 리그 MVP의 명예는 오타니 쇼헤이(Ohtani Shohei) 차지였다. 투구와 타격 둘 다 잘했기 때문이다. 투수 오타니(이후 ‘투타니’로 축약)는 130.1이닝을 소화해 156탈삼진에 평균자책점 3.18을 기록했다. 타자 오타니(이후 ‘타타니’로 축약)는 639타석에서 0.257/0.372/0.592/0.965의 슬래시라인과 46홈런 100타점 26도루로 시즌을 마무리했다.

여기서 오늘의 주제가 시작된다. 오타니가 자기 자신과 붙으면 어떻게 될까? 물리적인 제약은 둘째 치더라도, 야구에서 이 상황을 상상해볼 이유는 별로 없다. 아무리 뛰어난 선수도 투구와 타격 중에서 하나만을 월등히 잘하기 때문이다. ‘트라웃이 투수로서 자기 자신을 상대한다면?’ ‘디그롬이 타자로서 자기 자신을 상대한다면?’ 등 상상은 자유지만, 어느 한 쪽이 절대적으로 우세하기에 흥미가 생기지 않는다.

그렇지만 ‘이도류’ 오타니는 다르다. 투수로서 상대 타자들을 바보로 만들 능력도, 타자로서 상대 투수들을 낙담시킬 능력도 있기 때문이다.

막연한 공상에 머무르는 대신 정교한 사고실험으로 넘어가 보자. ‘투타니’가 지난해 마운드에서 보여준 모습은 ‘특정 결과가 발생할 확률’로 남았다. ‘타타니’도 마찬가지다. 확률이 전부 보여주지는 않지만, 확률만큼 선수를 최대한 나타낼 수단을 찾기도 어렵다. 확률을 투입할 몇 가지 공식을 살펴보고, 이를 이용해 21시즌 투타니와 21시즌 타타니를 가상으로 맞대결시켜보자.

오즈비(Odds Ratio)

타율 3할의 A타자와 피안타율 2할의 에이스 B투수가 맞대결한다. A타자의 타율은 어떻게 될까? 오즈비(Odds Ratio)를 활용하면 이 문제에 해답을 제시할 수 있다. 톰 탱고는 오즈비를 활용해 투타 맞대결 성적을 예측한 바 있다(링크). 피자 커터(러셀 칼튼)와 제라드 크로스 등 다른 분석가들 또한 투타 맞대결 성적 예측에 오즈비가 최적임을 암시한 바 있다(링크).

‘오즈’란 어떤 사건이 발생할 확률을 그 사건이 발생하지 않을 확률로 나눈 것이다. 예컨대 타율 3할의 ‘오즈’는 0.3/(1 – 0.3) = 3/7다. 달리 표현하면 타율 3할은 안타:아웃 비율이 3:7라는 뜻이며, 두 숫자를 각각 분자/분모에 넣으면 ‘오즈’가 된다. 오즈/(1+오즈)를 취하면 확률로 돌아온다. 우리가 찾는 “A타자가 B투수 상대로 안타를 칠 확률”은 아래와 같이 오즈 사이의 비율(‘오즈비’)을 이용해 구할 수 있다. 리그 평균 타율은 0.250으로 가정한다.

오즈(A가 B에게 안타 칠 확률)
= 오즈(A 타율) x 오즈(B 피안타율) / 오즈(리그 평균 타율*)
= {0.3/(1 – 0.3)} x {0.2/(1 – 0.2)} / {0.25/(1 – 0.25)} = 0.321
A가 B에게 안타 칠 확률 = 0.321/(1 + 0.321) = 약 0.243

‘투타니vs타타니’를 적용해보자. 앞으로 나오는 확률은 ‘손’을 감안한다. 투타니가 좌타자에게 던진 공이 ‘볼’이 될 확률은 36.8%다. 타타니가 우투수가 던진 공을 ‘볼’로 골라낼 확률은 40.9%다. 리그 전체 기준으로 우투수가 좌타자와 맞붙는 타석에서 투구 하나가 ‘볼’일 확률은 37%다. 이때 투타니가 타타니에게 ‘볼’을 던질 확률(혹은 타타니가 투타니를 상대해 ‘볼’을 골라낼 확률)은 아래와 같이 계산한다.

오즈(맞대결 ‘볼’ 확률)
= 오즈(투타니 ‘볼’ 확률) x 오즈(타타니 ‘볼’ 확률) / 오즈(리그 ‘볼’ 확률)
= {0.368/(1 – 0.368)} x {0.409/(1 – 0.409)} / {0.370/(1 – 0.370)} = 0.686
맞대결 ‘볼’ 확률 = 0.686/(1 + 0.686) = 약 0.407 = 40.7%

마르코프 체인(Markov Chain)

앞서 왜 ‘볼’의 확률을 계산했는지 의문을 품을 수 있다. 우리가 관심 있는 것은 타율, 출루율, 장타율 등이 아닌가? “3할의 A타자 vs 2할의 B투수” 예시에서도 봤듯이 타율, 출루율, 장타율 등을 계산하는 일이 불가능한 것도, 복잡한 것도 아니다. 오히려 단순하다는 장점이 있다.

그러나 실제 투타 맞대결은 ‘치거나 못 치거나’의 단순한 대결이 아니다. 볼 카운트라는 과정이 있기 때문이다. 초구에 결과가 결정되는 타석도 있지만, 볼 카운트가 전개되며 결과가 결정되는 타석이 훨씬 많다(ex. 1구 스트라이크 – 2구 볼 – 3구 파울(스트라이크) – 4구 파울 – 5구 삼진). 투타니와 타타니의 가상 맞대결도 이렇게 다채롭게 굴러가야 마땅하다.

오즈비를 통해 하나의 투구당 ‘볼’ ‘파울’ ‘스트라이크’ ‘안타’ 등등 확률의 구슬이 준비되었다. 이제 구슬들을 꿰어서 보배로 만들 차례다. 0-0 카운트는 0-1(스트라이크+파울), 1-0(볼) 그리고 타석 종료(삼진과 볼넷 제외) 중 한 상태로 귀결된다. 0-1 카운트는 0-2, 1-1 그리고 타석 종료(삼진과 볼넷 제외) 중 한 상태로 귀결된다. 타석이 종료되면 0-0 카운트로 돌아간다.

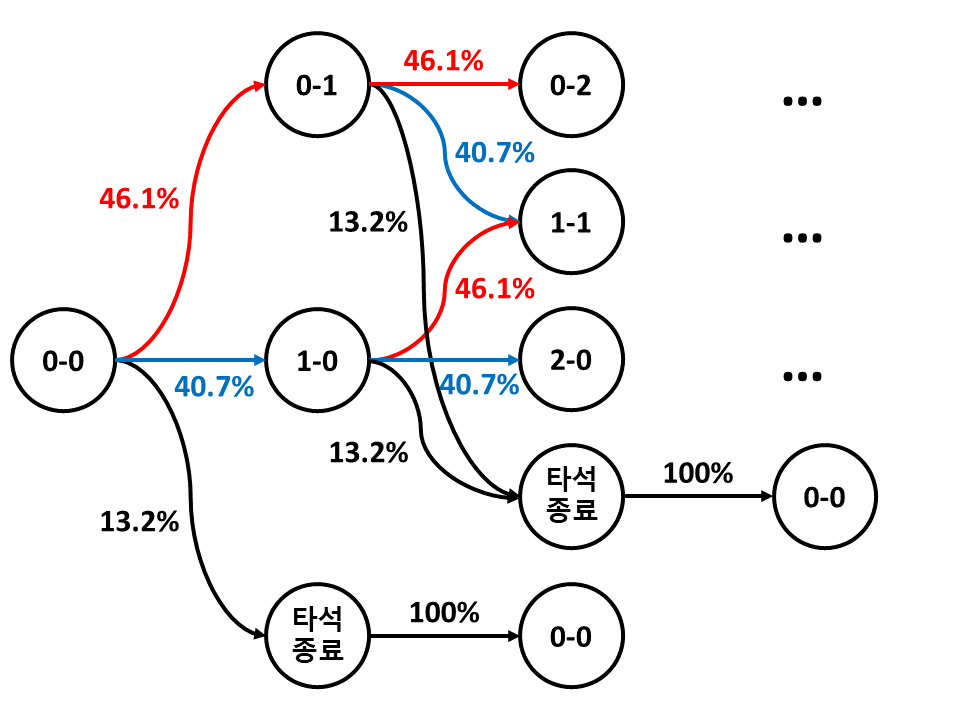
위의 관계는 아래 표(행렬)와 같이 나타낼 수 있다. 예를 들어 0-0 카운트에서 0-1이 될 확률은 왼쪽(행)에서 0-0, 위(열)에서 0-1에 해당하는 칸을 찾으면 된다. 스트라이크+파울의 확률의 합에 해당하는 46.1%임을 확인할 수 있다. 0-0 카운트에서 0-2가 될 확률은 왼쪽(행)에서 0-0, 위(열)에서 0-2에 해당하는 칸을 찾으면 된다. 0-0에서 공 한 개만으로 0-2가 될 수는 없으므로 확률은 0%이다. 다른 칸도 이와 같은 방법으로 각 칸마다 확률이 들어간다.

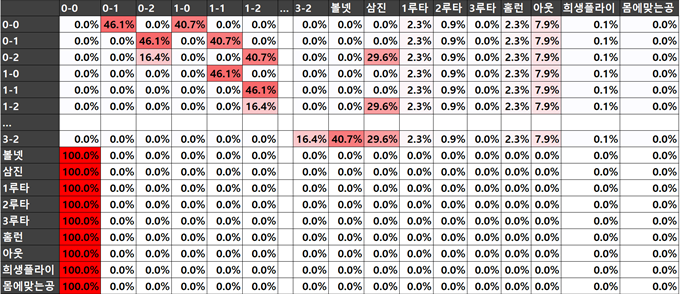
컴퓨터가 이 행렬을 거듭 계산하는 행위가 곧 투타니와 타타니의 가상 맞대결이다. 그리고 이 시뮬레이션(simulation) 방법을 마르코프 체인(Markov Chain)이라고 한다.

그래서 누가 이기는데 (1)

“그래서 누가 이기는데?”에 답할 준비를 마쳤다. 투타니와 타타니의 맞대결 예측은 오즈비를 통해 구현했다. ‘치거나 못 치거나’ 대신 볼도 고르고 파울도 내는 실제 대결 환경은 마르코프 체인을 이용해 조성했다. 스몰 샘플로 편향된 결과를 지양하기 위해 100타석짜리 표본을 총 5,000개 준비했다. 아래는 그 결과다.

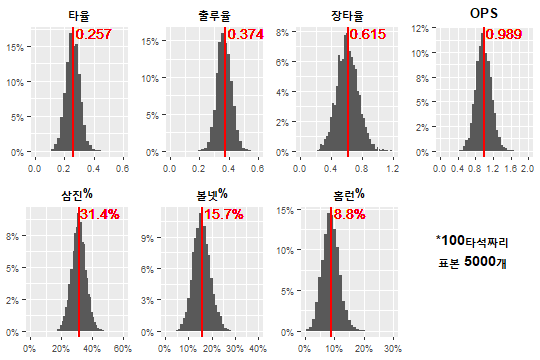
결과는 선명하다. 타타니의 완승이다. 타율이 다소 소박(?)하고 삼진을 자주 당하지만, 그럼 뭐 어떤가. OPS 모평균 추정치가 무려 0.990에 근접한다.

타타니가 투타니에게 완승을 거둔 이유가 무엇일까? 투타니의 좌타자 상대 스플릿에서 힌트를 찾을 수 있다(링크). 우리의 계산에 들어간 투타니는 ‘2021 투타니’가 아니라 ‘2021 좌타자 상대 투타니’다. 타타니가 좌타자이기 때문이다. 아쉽게도 ‘2021 좌타자 상대 투타니’는 리그 평균 수준의 투수였다. 타타니가 투타니를 압도한 것은 타자 오타니가 리그 평균 수준의 투수와 대결했기 때문이라고 볼 수 있다.

타타니의 완승을 선언하며 여기서 글을 끝내는 것도 가능하다. 하지만 이대로 끝내긴 아쉬우니 머리를 한 번 더 굴려보자. 투타니가 구사하는 구종은 꽤 독특하다(링크). 직구와 포크 비율이 월등히 높다. 반대로 투심 패스트볼과 체인지업은 전혀 던지지 않는다. 투타니와 타타니의 맞대결 예측에 이 구종 비율이 가중치로 반영되어야 하지 않을까?

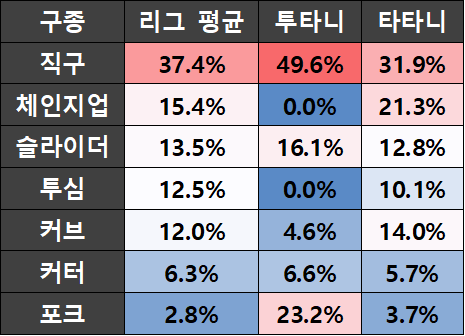
그래서 누가 이기는데 (2)

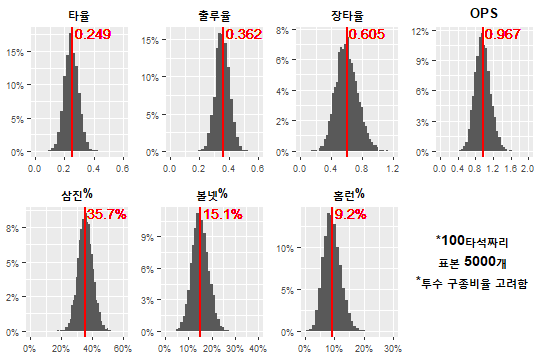
위는 투타니의 구종 비율을 가중치로 넣어 계산해본 결과다*. 여전히 결과는 선명하며, 타타니의 완승이다. 그러나 타타니가 조금 양보한 흔적을 찾을 수 있다. 타타니가 특정 구종을 상대할 때 예상되는 성적을 통해 이유를 찾아볼 수 있다.

*예를 들어 맞대결 시 ‘볼’의 오즈는 다음과 같이 계산된다. {(투타니 직구 투구수/투타니 전체 투구수)*오즈(투타니 직구 볼)*오즈(타타니 직구 볼)/오즈(리그 직구 볼)} + {(투타니 포크 투구수/투타니 전체 투구수)*오즈(투타니 포크 볼)*오즈(타타니 포크 볼)/오즈(리그 포크 볼)} + …

직구 상대 OPS* = 0.886
포크 상대 OPS* = 0.592
투심 상대 OPS* = 1.157
체인지업 상대 OPS* = 0.993
*엄밀하게 표현하자면 OPS(투타니 입장에서 피OPS) 모평균 추정치다.

투타니가 가장 많이 던진 직구 상대로 타타니는 인간적(?)인 모습이었다. 투타니가 두번째로 많이 던진 포크는 타타니가 손도 못 쓴 구종이다. 타타니가 강했던 구종은 투심과 체인지업이었는데, 투타니는 두 구종을 1구도 던지지 않았다. 종합하자면 투타니가 던지는 구종들은 나름 타타니의 약점에 최적화되었다. 타타니의 승리를 막기 역부족이었지만 말이다.

번외

글의 최초 의도는 아니었으나, 그림을 통해 분포의 개념을 간접적으로 체험할 수 있다. 투수와 타자가 애초에 커리어 내내 100타석씩 맞붙기는 쉽지 않다. 적지 않은 횟수에도 불구하고 타율(혹은 피안타율)이 1할이 되지 않는 평행 우주도, 4할이 넘는 평행 우주도 발생했다.

내친김에 중계방송 및 기사에서 흔히 쓰는 시즌 단위로 구현을 해보자. 넉넉하게 인심 써서 20타석씩 맞붙여봤다. 각 그림의 가로축을 보면 범위가 얼마나 넓게 퍼져 있는지 알 수 있다. ‘올 시즌 상대 전적 5할‘ 등 멘트는 흥미를 자아내기 충분하지만, 이를 곧이곧대로 ‘신호’로 받아들이고 분석과 주장의 근거로 삼는 것이 얼마나 위험한지 느낄 수 있다.

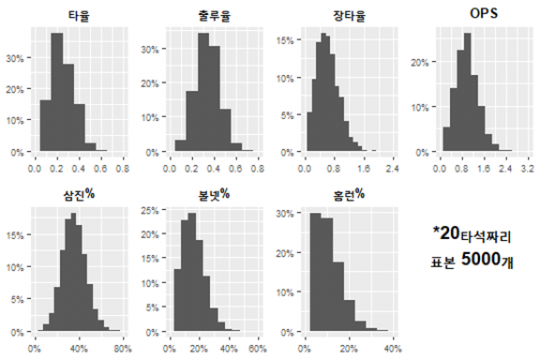
참고=Baseball Reference, Baseball Savant
야구공작소 곽창현 칼럼니스트
에디터=야구공작소 오연우, 장원영, 서주오, 유은호
일러스트=야구공작소 이찬희

ⓒ야구공작소. 출처 표기 없는 무단 전재 및 재배포를 금합니다. 상업적 사용은 별도 문의 바랍니다.